はじめに
この記事は弊研究室の某課題について考えるの23日目の記事です。
今日はハッシュ関数について簡単な解説をします。
ハッシュ関数とは
あるデータが与えられた場合にそのデータを代表する数値を得る操作、または、その様な数値を得るための関数のことを指します。HashMap関数とかSHA1とかに代表されるようなやつらです。
国の識別にJPとか使いますがこれはJapanとわかるので一種のハッシュ値と言えるでしょう
ハッシュ関数の用途
ハッシュの用途としては以下のような感じです
- ハッシュテーブル
- キャッシュ
- 重複レコードの検出
- 類似レコードの探索
- 幾何学的ハッシュ
- 改ざんの検出
この記事では改ざんの検出に扱われるハッシュについて焦点をあて記述していきます
改ざんの検出
ファイルの信頼性を確かめる際に,同じファイルを比較するのは(ファイルにもよりますが)コストが重くなります。そこで元のファイルのハッシュを計算しておき,そのハッシュ値と比較したいファイルのハッシュ値を比較することでファイルの信頼性を保証できます。ハッシュ値を計算するハッシュ関数は高速なためファイル同士を比較するよりも高速に検証可能です。
改ざんの検出を行う際は簡単なハッシュ関数であると,同じハッシュ値を求めることが可能なため,安全なハッシュ関数を用いる必要があります。
ハッシュの特性
ハッシュ関数が安全であるかは以下の特性が守られているかにかかっています。
- 原像計算困難性
- 弱衝突耐性(第2原像計算困難性)
- 強衝突耐性(衝突困難性)
それぞれは原像計算困難 ⊃ 弱衝突耐性 ⊃ 強衝突耐性な関係性です
原像計算困難性
定義:ハッシュ値Hに対してH=h(m)となるmを求められない
これは単純であるハッシュ値がわかったときにそのハッシュ値と同じになるmを求められてはいけないということです。
弱衝突耐性
定義:h(m)からh(m)=h(n)を満たすnを求められない
弱衝突耐性がないと下の画像にある?を求められるということになります。
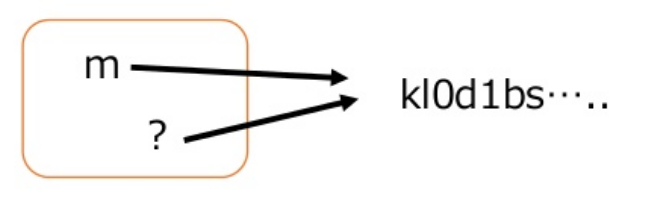
強衝突耐性
定義:h(m)≠h(n)となるmとnを求められない
強衝突性がないとmとnを見つけられる。作れるということになります。
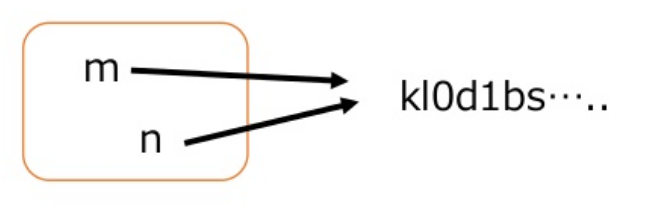
よく知られているハッシュ関数
このうち推奨暗号なのはsha2だけです。新しくシステム実装する際に使うときには基本的にsha2を使いましょう。
Shattered Attack (蛇足)
蛇足です。去年Googleが公開したSHA1の脆弱性の話ですね!
今までさんざん危ない危ない言われてたけど衝突性は破られていなかったSHA1の強衝突耐性が破られたという話です。
これを利用した問題がSECCONで出ました。まぁ仕組みに関しては昔私がLTで話したので読んでね(露骨なアクセス数稼ぎ)
www.slideshare.net
Length Extention Attack
レングスエクステンションアタックとは攻撃者があるハッシュ値を入手した際に元のメッセージに任意のメッセージを付与したハッシュ値を導出可能という攻撃方法です。
ちなみにこの攻撃方法は反復型ハッシュ関数の、H(M||M')がH(M)とM'から計算できるという性質を利用する攻撃です。
md5やsha1,sha2といったMerkle-Damgård構造のハッシュ関数は反復型ハッシュ関数であるため攻撃可能なケースが存在します。
HashPumpというツールがあります。このツールではMD5,SHA1,SHA256,SHA512に対応しています。オリジナルのハッシュ関数は自力で攻撃コードを書く必要があります